专门考察并查集的题目并不算多，与之前的专题相比，他不像是一类解决问题的思路，倒更像是一个工具，帮助我们给元素分组，分成不同的“帮派”，并可以方便的查找某两个元素是否是同一个组别中。

今天参加了一个ACM比赛，说实话自己接触算法不多，还是最近准备机试才开始刷题之旅，但从比赛的结果来看，确实也有很多的收获。最大的收获应该算是对于最近努力的肯定，让我有了更多的自信和坚持下去的动力。

说回比赛，中间有一道题目，运用了克鲁斯卡尔生成树算法的思想，其中很重要的一部分是并查集的运用，在好容易完成代码的编写后提交却发现超时，换思路肯定是太费劲了，突然想到之前看到过不同的优化并查集的思路，于是当即翻出来加进代码，果然AC。第一次意识到是否优化代码的显著差别，时间差了将近十倍，也意识到了并查集优化的重要性，于是决定开专题将之前的学习笔记写下来，以便日后查阅。

并查集的目的

简单的一句话——元素分组。
通过并查集，我们可以快速记录元素分组，并快速查询元素是否在同一分组中，这便是并查集最基础的使用目的。在克鲁斯卡尔算法中，我们用来判断是否当前剩下的最短边的起止结点在同一个连通分量中。

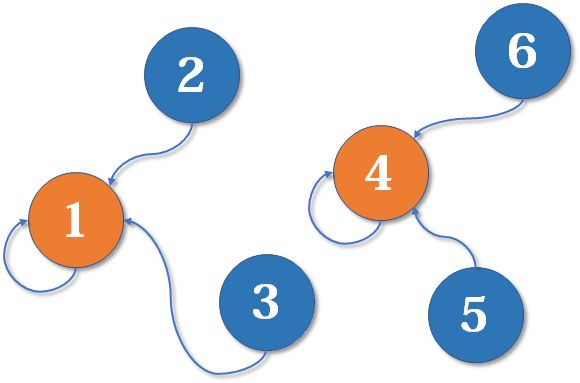
而为了实现这一目的，要说到并查集的两个基本操作

基本操作：

1. 合并
2. 查询

这就是并查集的两个最基本的操作，通过这两个操作，我们就能实现对元素的分组操作。

三个要素

• 初始化
  开始时，我们需要初始化将所有元素的根元素设为自己，也就是每个元素自立帮派。

• 元素查询
  要查询两个元素是否属于同一个分组，我们只需要查询他的根元素（帮主）是否是同一个人。

• 元素合并
  相应的，要实现元素合并，就要选两个元素中的任意一个帮主，认另一个帮主作帮主（也就是当他的小弟！），这样我们之后查询两个元素的帮主应该就是同一个元素，我们也就认为他们是同一个分组。

我们直接上代码块理解并查集的这三个要素，实现了这三个要素，也就有了最基本的并查集，当然后期还有很大的优化空间。

• 初始化（每个人都做自己的帮主）

int fa[MAXN];
inline void init(int n)
{
    for (int i = 1; i <= n; ++i)
        fa[i] = i;
}

• 查询（递归）

int find(int x)
{
    if(fa[x] == x) //如果帮主是自己
        return x;
    else
        return find(fa[x]); //否则就去找帮主的帮主
}

• 合并

inline void merge(int i, int j)
{
    fa[find(i)] = find(j);
}

这样我们就写出了一个最基本的并查集，然而这个并查集还有很多需要优化的地方。

优化

问题一：路径太长（压缩路径）

如果我们每次合并都只是单纯的让帮主认作别人的小弟，那么底下的小弟就需要通过多次查询才能找到自己真正的帮主，这就是这个并查集存在的第一个问题：查询的路径太长。

我们可以压缩路径来解决这个问题，如果有一个元素存在帮主，我们就在查询的过程中将他的父元素设置为他的帮主，这样在之后的查询过程中就可以一次查询到根元素。
体现在代码中就是查询的代码发生了变化：

int find(int x)
{
    return x == fa[x] ? x : (fa[x] = find(fa[x]));
}

当然这样的解决方案存在一个小小的弊端，就是只有在第一次查询之后路径才会被压缩，而不是建立的时候就已经压缩完成。

问题二：生成的树太高（按秩合并）

之前在说到在并查集元素合并的时候，两个元素任意选择一个作为新的帮主，这就会引发一个问题，我们生成的查找分组的树可能会变的很高很不平衡，我们可以引入一个新的数组记录所有元素下面的层数（秩数），在合并时，只需要让秩数较小的元素认秩数大的元素为帮主即可；如果两个元素秩数相同，只需要一个认另一个帮主，再将新的帮主秩数加一即可。

初始化加入变量

inline void init(int n)
{
    for (int i = 1; i <= n; ++i)
    {
        fa[i] = i;
        rank[i] = 1;    //引入新的变量
    }
}

新的合并函数

inline void merge(int i, int j)
{
    int x = find(i), y = find(j);    //先找到两个根节点
    if (rank[x] <= rank[y])
        fa[x] = y;
    else
        fa[y] = x;
    if (rank[x] == rank[y] && x != y)
        rank[y]++;                   //如果深度相同且根节点不同，则新的根节点的深度+1
}

时间复杂度

并查集并不是一个二叉树，而是一个多叉树，所以并查集的 查询和合并 时间复杂度并不是 $O(\log n)$，在加上 rank 和路径压缩优化后 ，并查集的时间复杂度为 $O(\alpha(n))$，其中 $\alpha$ 为阿克曼函数的反函数。这里需要注意并查集的建立是 $n$ 次合并操作，所以并查集的时间复杂度为 $O(n\alpha(n))$。

$O(\log^* n)$ 是指迭代对数函数，通常被认为是阿克曼函数的反函数在复杂性分析中的一个应用。迭代对数 $\log^*n$的定义是对给定的正整数 $n$，我们需要对 $n$ 迭代应用对数函数多少次才能得到的值不大于 1。这个函数增长非常慢，在算法分析中出现 $O(\log^* n)$ 通常意味着算法非常高效。这种函数通常用于分析某些高度优化的数据结构的性能，比如不相交集合数据结构（Disjoint Set Union-Find）中使用路径压缩和按秩合并的优化技术。

参考

• https://zhuanlan.zhihu.com/p/93647900
• https://blog.csdn.net/yuzhiqiang666/article/details/80721436