什么是单调栈

顾名思义，单调栈就是满足单调性的栈结构，只在一端进行元素进出，后进先出，所以用栈维护（区别于单调队列）。

单调栈的应用场景是：在一个数组中，找到每个元素的左边/右边离它 最近的 比它大/小的元素。

以下面的图为例，我们要找到每个元素的右边离它最近的比它 大 的元素（739.每日温度）。那么我们可以从右往左遍历，维护一个单调递减的栈，当遍历到一个元素 a 时，如果栈顶元素 b 比 a 大，那么栈顶元素 b 就是 a 右边最近的比 a 大的元素，加入答案并加入 a，如果栈顶元素 b 小于等于 a，那么就一直出栈（因为 b 不可能是大于 a 左侧任何元素的右边最近的元素了，所以可以放心的删除），直到栈顶元素比它大，或者栈为空，然后把当前元素入栈。

这里遍历每个元素后，单调栈始终保持两个性质：

1. 当前元素必会加入栈内
2. 栈内元素单调递减

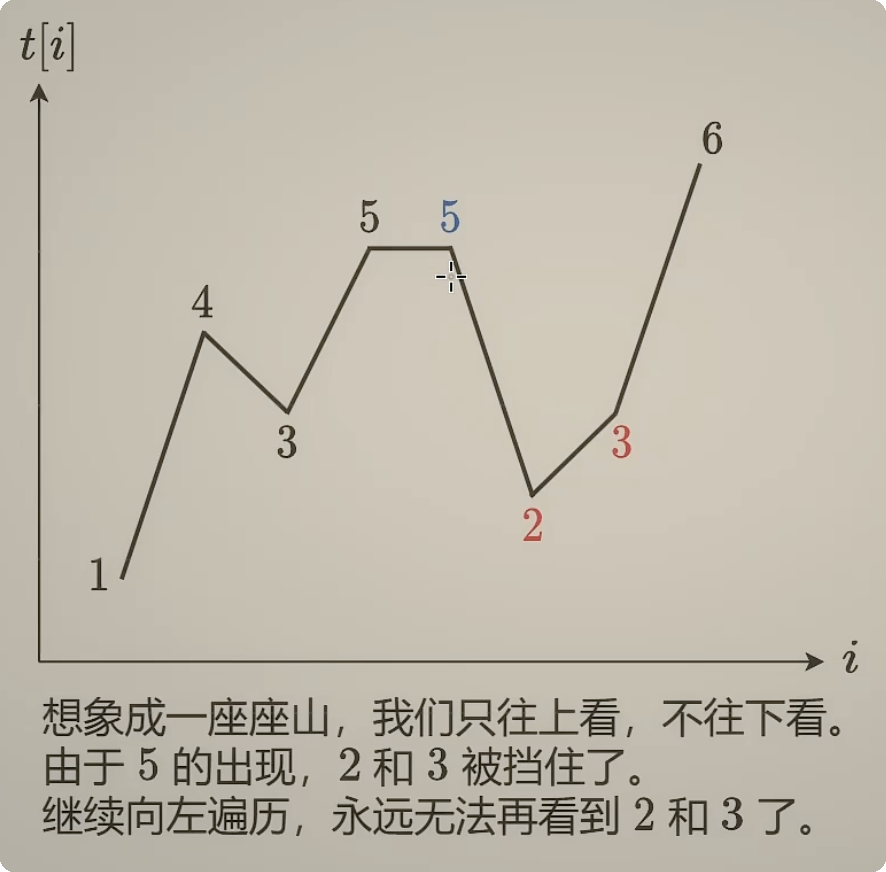
从上面的思路也可以看出，单调栈就是通过维护一个满足单调性的栈，来删除一些不可能成为答案的元素，从而减少一些不必要的计算。

class Solution:
    def dailyTemperatures(self, temperatures: List[int]) -> List[int]:
        n = len(temperatures)
        ans = [0] * n

        st = []
        for i in range(n - 1, -1, -1):  # 倒序
            t = temperatures[i]
            while st and temperatures[st[-1]] <= t:
                st.pop()
            if st:
                ans[i] = st[-1] - i   # 直到弹栈后记录答案
            st.append(i)
        
        return ans

这个题目还可以用正序的单调栈实现，二者的区别就是倒序在遍历到一个元素时，一定会沿着要求的方向（右）一直找到一个比它大的元素（直到栈为空）；而正序的单调栈，是在遍历的元素大于栈顶元素时弹栈的过程中记录答案的。

class Solution:
    def dailyTemperatures(self, temperatures: List[int]) -> List[int]:
        n = len(temperatures)
        ans = [0] * n

        st = []
        for i in range(n):  # 正序
            t = temperatures[i]
            while st and temperatures[st[-1]] < t:
                ans[st[-1]] = i - st[-1]    # 在弹栈的过程中给弹出的元素记录答案
                st.pop()
            st.append(i)
        return ans

题目

2454. 下一个更大元素 IV

这题要找「下下个更大元素」。和上面说的找下一个更大元素的不同是，我们需要再维护另一个 单调递减 单调栈 biggerMet，存储已经遇到过比他大的数的数，也就是说在第一个 单调递减 单调栈 stack 内被弹出的数，会加入第二个单调栈。当遍历下一个数字 $num$ 时，首先判断是否比 biggerMet 的栈顶元素大，如果是，那么这个数 $num$ 就是 biggerMet 栈顶元素的下一个更大元素，加入答案，然后弹出 biggerMet 栈顶元素，直到栈顶元素比 $num$ 大，或者栈为空。
接着维护第一个单调栈 stack，如果 $num$ 比栈顶元素大，那么 $num$ 就是栈顶元素的下一个更大元素，加入答案，然后弹出栈顶元素，直到栈顶元素比 $num$ 大，或者栈为空。
这里需要注意从 stack 到 biggerMet 的元素需要接在 biggerMet 的栈顶元素后面，同时为了保证单调性，需要在 stack 中找到第一个比 $num$ 大的元素，然后把这个元素后面的所有元素加入 biggerMet。

class Solution:
    def secondGreaterElement(self, nums: List[int]) -> List[int]:
        biggerMet = []
        ret = [-1] * len(nums)
        stack = []
        for i, num in enumerate(nums):
            while biggerMet and nums[biggerMet[-1]] < num:
                ret[biggerMet.pop()] = num
            j = len(stack) - 1
            while j >= 0 and nums[stack[j]] < num:
                j -= 1
            biggerMet += stack[j + 1:]
            del stack[j + 1:]
            stack.append(i)
        
        return ret

901. 股票价格跨度

设计一个算法收集某些股票的每日报价，并返回该股票当日价格的 跨度 。

当日股票价格的 跨度 被定义为股票价格小于或等于今天价格的最大连续日数（从今天开始往回数，包括今天）。

class StockSpanner {
    Deque<int[]> q;
    public StockSpanner() {
        this.q = new ArrayDeque<>();
    }

    public int next(int price) {
        int cnt = 0;    // 当前价格左侧连续比它小的元素个数
        while (!q.isEmpty() && q.peek()[0] <= price) {
            cnt += q.pop()[1];
            cnt++;
        }
        q.push(new int[]{price, cnt});
        return q.peek()[1] + 1;
    }
}

/**
 * Your StockSpanner object will be instantiated and called as such:
 * StockSpanner obj = new StockSpanner();
 * int param_1 = obj.next(price);
 */

42. 接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

这个题目的思路可以概括为：找上一个更大的元素，在找的过程中填坑，这样使用横向填面积的方式来计算答案。

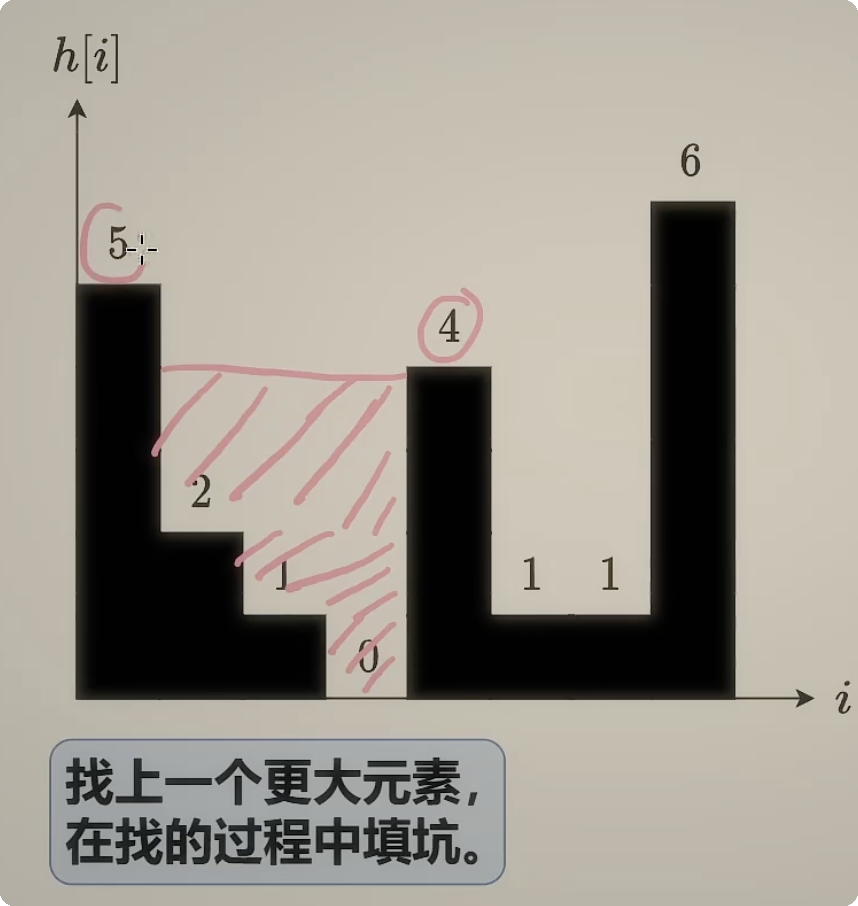
class Solution:
    def trap(self, height: List[int]) -> int:
        n = len(height)
        ans = 0
        st = []
        for i in range(n):
            h = height[i]
            while st and height[st[-1]] < h:
                bottom = height[st.pop()]
                if not st: break
                vol = (min(height[st[-1]], h) - bottom) * (i - st[-1] - 1)
                ans += vol
            st.append(i)
        return ans

参考

• 灵茶山艾府：单调栈
• OI wiki