avatar

🧊foril

giteegiteegiteegitee
avatar

🧊foril

基环树

2023-10-02 -

什么是基环树

基环树是一个连通图，有 nn 个点和 nn 条边，相比于树的 nn 个点与 n−1n - 1 条边，会多出一个环（有且只有一个环），所以称为基环树。
多颗基环树也符合 nn 个点和 nn 条边的定义，由多棵基环树组成的森林称作基环森林。
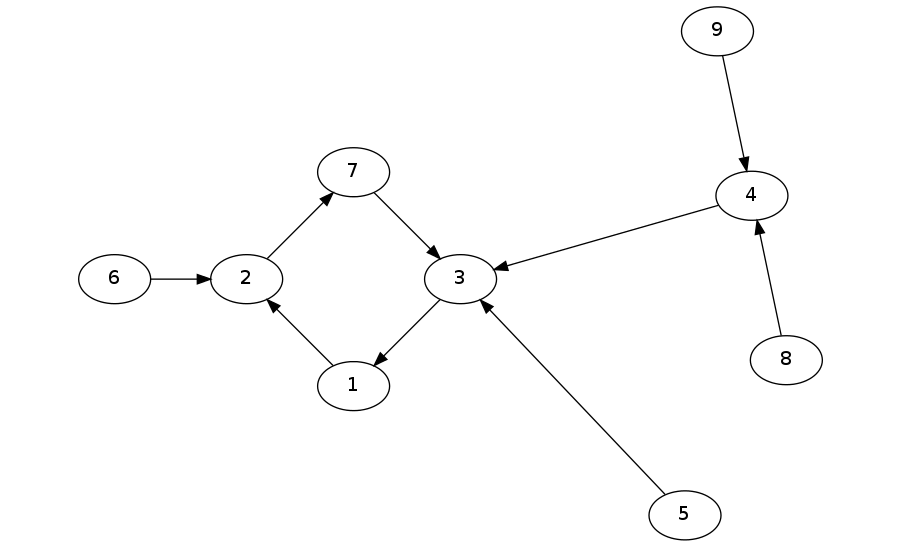
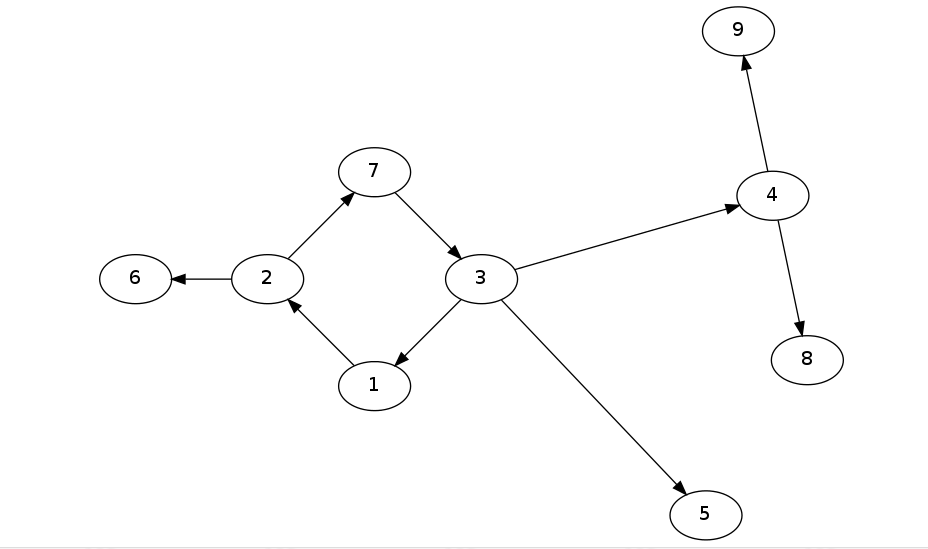
有向的基环树还可以分为 in-tree（内向树） 和 out-tree（外向树），分别是每个点出度为 11 以及每个点入度为 11 的基环树，直观的可以看出内向树的边都指向里，外向树的边都指向外。

内向树 内向树

对应的外向树 外向树

解决思路

关于基环树的经典题型主要有 基环树直径、基环树两点之间距离，基环树DP 等。

基环树问题的通用处理方法是通过一次拓扑排序「剪掉」所有树枝，因为拓扑排序后，树枝节点的入度均为 00，基环节点的入度均为 11。这样就可以将基环和树枝分开，从而简化后续处理流程。

例题

2127. 参加会议的最多员工数

一个公司准备组织一场会议，邀请名单上有 nn 位员工。公司准备了一张圆形的桌子，可以坐下 任意数目 的员工。

员工编号为 00 到 n−1n - 1 。每位员工都有一位 喜欢 的员工，每位员工 当且仅当 他被安排在喜欢员工的旁边，他才会参加会议。每位员工喜欢的员工 不会 是他自己。

给你一个下标从 00 开始的整数数组 favorite ，其中 favorite[i] 表示第 ii 位员工喜欢的员工。请你返回参加会议的 最多员工数目。

思路

具体详见 灵茶山艾府：内向基环树：拓扑排序 + 分类讨论， 附上代码加注释：

class Solution:
    def maximumInvitations(self, favorite: List[int]) -> int:
        n = len(favorite)
        deg = [0] * n
        for f in favorite:
            deg[f] += 1  # 统计基环树每个节点的入度

        max_depth = [1] * n
        q = deque(i for i, d in enumerate(deg) if d == 0)
        while q:  # 拓扑排序，剪掉图上所有树枝
            x = q.popleft()
            y = favorite[x]  # x 只有一条出边
            max_depth[y] = max_depth[x] + 1
            deg[y] -= 1
            if deg[y] == 0:
                q.append(y)

        max_ring_size = sum_chain_size = 0
        for i, d in enumerate(deg):
            if d == 0: continue

            # 遍历基环上的点
            deg[i] = 0  # 将基环上的点的入度标记为 0，避免重复访问
            ring_size = 1  # 基环长度
            x = favorite[i]
            while x != i:
                deg[x] = 0  # 将基环上的点的入度标记为 0，避免重复访问
                ring_size += 1
                x = favorite[x]

            if ring_size == 2:  # 基环长度为 2
                sum_chain_size += max_depth[i] + max_depth[favorite[i]]  # 累加两条最长链的长度
            else:
                max_ring_size = max(max_ring_size, ring_size)  # 取所有基环长度的最大值
        return max(max_ring_size, sum_chain_size)

2876. 有向图访问计数

现有一个有向图，其中包含 nn 个节点，节点编号从 00 到 n−1n - 1。此外，该图还包含了 nn 条有向边。

给你一个下标从 00 开始的数组 edges ，其中 edges[i] 表示存在一条从节点 ii 到节点 edges[i] 的边。

想象在图上发生以下过程：

你从节点 x 开始，通过边访问其他节点，直到你在 此过程 中再次访问到之前已经访问过的节点。 返回数组 answer 作为答案，其中 answer[i] 表示如果从节点 ii 开始执行该过程，你可以访问到的不同节点数。

思路

对于在基环上的点，其可以访问到的节点数，就是基环的大小。 对于不在基环上的点 x，其可以访问到的节点数，是基环的大小，再加上点 x 的深度。这里的深度是指以基环上的点 rootroot 为根的树枝作为一棵树，点 x 在这棵树中的深度。这可以从 rootroot 出发，在反图上 DFS 得到。

注意题目给出的图可能不是连通的，可能有多棵内向基环树。

class Solution:
    def countVisitedNodes(self, g: List[int]) -> List[int]:
        n = len(g)
        rg = [[] for _ in range(n)]  # 反图
        deg = [0] * n
        for x, y in enumerate(g):
            rg[y].append(x)
            deg[y] += 1

        # 拓扑排序，剪掉 g 上的所有树枝
        # 拓扑排序后，deg 值为 1 的点必定在基环上，为 0 的点必定在树枝上
        q = deque(i for i, d in enumerate(deg) if d == 0)
        while q:
            x = q.popleft()
            y = g[x]
            deg[y] -= 1
            if deg[y] == 0:
                q.append(y)

        ans = [0] * n
        # 在反图上遍历树枝
        def rdfs(x: int, depth: int) -> None:
            ans[x] = depth
            for y in rg[x]:
                if deg[y] == 0:  # 树枝上的点在拓扑排序后，入度均为 0
                    rdfs(y, depth + 1)
        for i, d in enumerate(deg):
            if d <= 0:
                continue
            ring = []
            x = i
            while True:
                deg[x] = -1  # 将基环上的点的入度标记为 -1，避免重复访问
                ring.append(x)  # 收集在基环上的点
                x = g[x]
                if x == i:
                    break
            for x in ring:
                rdfs(x, len(ring))  # 为方便计算，以 len(ring) 作为初始深度
        return ans

参考