字典树，顾名思义，就是一个像字典一样的树。

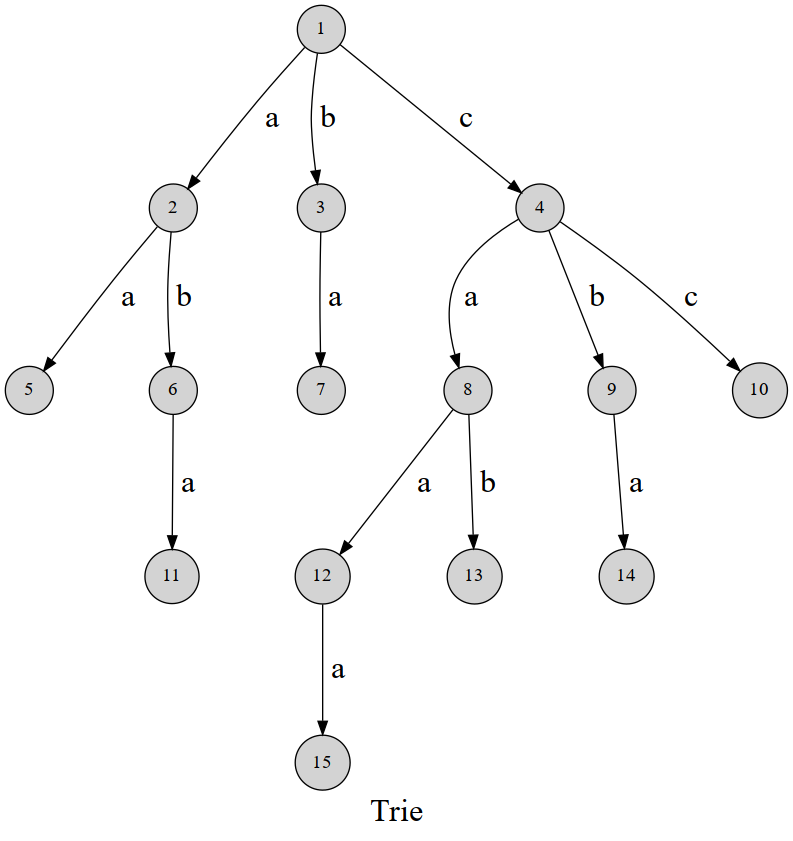
Trie 的核心思想是空间换时间。利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。

Trie 树实际上是一个确定有限状态自动机(DFA)，通常用转移矩阵表示。行表示状态，列表示输入字符，（行，列）位置表示转移状态。这种方式的查询效率很高，但由于稀疏的现象严重，空间利用效率很低。也可以采用压缩的存储方式（即链表）来表示状态转移，但由于要线性查询，会造成效率低下。

基本性质

前缀树的 3 个基本性质：

1. 根节点不包含字符，除根节点外每一个节点都只包含一个字符。
2. 从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串。
3. 每个节点的所有子节点包含的字符都不相同。

Trie 树的实现

实现字典树，需要定义如何插入新的字符串以及如何查找字符串。

实现一：

字典树的第一种实现方式是利用一个类或结构体，每个节点需要记录下一个转移的所有可能的字符，以及是否是一个单词的结尾。

class Trie {
private:
    vector<Trie*> children;
    bool isEnd;

public:
    Trie() : children(26), isEnd(false) {}

    void insert(string word) {
        Trie* node = this;
        for (char ch : word) {
            ch -= 'a';
            if (node->children[ch] == nullptr) {
                node->children[ch] = new Trie();
            }
            node = node->children[ch];
        }
        node->isEnd = true;
    }

    bool search(string word) {
        Trie* node = this;
        for (char ch : prefix) {
            ch -= 'a';
            if (node->children[ch] == nullptr) {
                return nullptr;
            }
            node = node->children[ch];
        }
        return node != nullptr && node->isEnd;
    }
};

实现二：

Trie 树的第二种实现方案，是利用一个二维数组，数组的每一行表示一个节点，每一列表示一个转移，如果某个节点有一个转移，那么就在对应的列上标记为下一个节点的编号，如果没有转移，就标记为 0。

struct trie {
  int nex[100000][26], cnt;
  bool exist[100000];  // 该结点结尾的字符串是否存在

  void insert(char *s, int l) {  // 插入字符串
    int p = 0;
    for (int i = 0; i < l; i++) {
      int c = s[i] - 'a';
      if (!nex[p][c]) nex[p][c] = ++cnt;  // 如果没有，就添加结点
      p = nex[p][c];
    }
    exist[p] = 1;
  }

  bool find(char *s, int l) {  // 查找字符串
    int p = 0;
    for (int i = 0; i < l; i++) {
      int c = s[i] - 'a';
      if (!nex[p][c]) return 0;
      p = nex[p][c];
    }
    return exist[p];
  }
};

Trie 树的应用

字典树的常见应用包括 检索字符串（查找一个字符串是否在「字典」中出现过）、维护异或极值（在一组数中，找出与给定数异或值最大的数）以及 维护异或和（在一组数中，找出与给定数异或值最小的数）等，也可以用在自动补全、拼写检查、IP 路由等领域。

例题

421. 数组中两个数的最大异或值

给你一个整数数组 nums ，返回 nums[i] XOR nums[j] 的最大运算结果，其中 $0 \leq i \leq j < n$。 提示：$1 \leq nums.length \leq 2 * 10^5$

根据题目 $n$ 的范围，我们可以知道，暴力枚举的时间复杂度是 $O(n^2)$，会超时。

所以我们使用字典树，利用字符串的公共前缀来减少查询时间，也就是针对一个数字，能够在 $O(1)$ 的时间复杂度内找到出现过的数字中与它异或值最大的数字。

这里需要注意的几个技巧：

1. 要保证在查找时， 字典树内至少有一个数，所以需要先插入一个数，再查找。
   如果查找时字典树内没有数，那么在往下一层查找时，会出现空指针异常。
   这里的字典树是一棵等高的树，没有记录终点，所以在每一层查找时肯定可以找到一个数。
2. 从高位到低位找最大异或值。

class Trie {
public:
    Trie* zero;
    Trie* one;
};
class Solution {
private:
    Trie* root = new Trie();
    static constexpr int HIGH_BIT = 30;
public:
    void add(int num) {
        Trie* node = root;
        for (int i = HIGH_BIT; i>-1; i--) {
            if (((num >> i) & 1) == 1) {
                if (node->one == nullptr) {
                    node->one = new Trie();
                }
                node = node->one;
            } else {
                if (node->zero == nullptr) {
                    node->zero = new Trie();
                }
                node = node->zero;
            }
        }
    }

    int check(int num) {
        Trie* cur = root;
        int x = 0;
        for (int k = HIGH_BIT; k >= 0; --k) {
            int bit = (num >> k) & 1;
            if (bit == 0) {
                // a_i 的第 k 个二进制位为 0，应当往表示 1 的子节点 right 走
                if (cur->one) {
                    cur = cur->one;
                    x = x * 2 + 1;
                }
                else {
                    cur = cur->zero;
                    x = x * 2;
                }
            }
            else {
                // a_i 的第 k 个二进制位为 1，应当往表示 0 的子节点 left 走
                if (cur->zero) {
                    cur = cur->zero;
                    x = x * 2 + 1;
                }
                else {
                    cur = cur->one;
                    x = x * 2;
                }
            }
        }
        return x;
    }
    int findMaximumXOR(vector<int>& nums) {
        int res = 0;
        for (int i = 1; i < nums.size(); i++) {     // 从下标为 1 的数开始，保证字典树中至少有两个数
            add(nums[i - 1]);
            res = max(res, check(nums[i]));
        }
        return res;
    }
};

2935. 找出强数对的最大异或值 II

给你一个下标从 $0$ 开始的整数数组 nums 。如果一对整数 $x$ 和 $y$ 满足以下条件，则称其为 强数对 ：

你需要从 nums 中选出两个整数，且满足：这两个整数可以形成一个强数对，并且它们的按位异或（XOR）值是在该数组所有强数对中的 最大值 。

返回数组 nums 所有可能的强数对中的 最大 异或值。

注意，你可以选择同一个整数两次来形成一个强数对。

上面那个题只需要求出数组中两个数的最大异或值，而这个题对两个数做了一定限制，即两个数的差值不能超过两个数中的最小值。

给两个数加入限制后，总体思路是一致的，使用字典树从高位到低位找最大异或值即可，区别就是需要对数组排序后维护一个滑动窗口，保证窗口内的数满足条件，然后把窗口左边的数字 移除，这里的重要区别就在这里怎么移除。

通过维护一个计数器，每次插入一个数，就把这个数的计数器加一，每次移除一个数，就把这个数的计数器减一，就可以实现对数字的移除。

class Solution {
    Trie root = new Trie();
    static final int HIGH_BIT = 20;
    void add(int num) {
        Trie curr = root;
        for (int i = HIGH_BIT; i > -1; i--) {
            int bit = num >> i & 1;
            if (curr.children[bit] == null) {
                curr.children[bit] = new Trie();
            }
            curr = curr.children[bit];
            curr.cnt += 1;
        }
    }
    void remove(int num) {
        /** 从 root 中删除 num
         * 要求 num 必须已经在 root 中，不额外检查
         */
        Trie curr = root;
        for (int i = HIGH_BIT; i > -1; i--) {
            int bit = num >> i & 1;
            curr = curr.children[bit];
            curr.cnt -= 1;
        }
    }
    int check(int num) {
        Trie curr = root;
        int xor_res = 0;
        for (int i = HIGH_BIT; i > -1; i--) {
            int bit = num >> i & 1;
            if (curr.children[bit ^ 1] != null && curr.children[bit ^ 1].cnt > 0) {
                xor_res |= 1 << i;
                curr = curr.children[bit ^ 1];
            } else {
                curr = curr.children[bit];
            }
        }
        return xor_res;
    }
    public int maximumStrongPairXor(int[] nums) {
        Arrays.sort(nums);
        int ret = 0;

        // 滑动窗口
        int left = 0;
        for (int y : nums) {
            add(y);
            while (nums[left] * 2 < y) {
                remove(nums[left++]);
            }
            ret = Math.max(ret, check(y));
        }
        // 下面这段代码存在的问题是如果第一个数字和第二个数字不是强数对，i = 1 时 nums[0] 会被删去，root 下只有一棵🌲，check 的时候取另一个方向会取到 null，所以先把自己放进去，就可以保证不会错
        // add(nums[0]);   // 把 0 放进去
        // for (int i = 1; i < nums.length; i++) {
        //     while (nums[left] * 2 < nums[i]) {
        //         remove(nums[left++]);
        //     }
        //     // 找最大异或值
        //     ret = Math.max(ret, check(nums[i]));
        //     add(nums[i]);
        // }
        return ret;
    }
}

class Trie {
    Trie[] children = new Trie[2];
    int cnt = 0;
}

参考

• Wiki
• 知乎：数据结构与算法：字典树（前缀树）
• OI Wiki