🧊foril

🧊foril

差分数组

2023-09-30

阅读时间：12分钟

差分数组的实质（difference array）其实就是记录每个位置相对于前一个位置数量的 变化量（difference），这样针对于一个子数组的操作（数量的统一变化）就可以通过对两个数的操作实现。
其核心思想是将对一个连续子数组的增/减操作，转化为对子区间端点的增/减操作，以 $O(1)$ 的时间对每次操作进行记录，最终在通过累加 difference 得到最终的数组。

题单

首先来看一个差分数组的裸题。

1094. 拼车

车上最初有 capacity 个空座位。车只能向一个方向行驶（也就是说，不允许掉头或改变方向）

给定整数 capacity 和一个数组 trips , $trip[i] = [numPassengers_i, from_i, to_i]$ 表示第 $i$ 次旅行有 $numPassengers_i$ 位乘客，接他们和放他们的位置分别是 $from_i$ 和 $to_i$ 。这些位置是从汽车的初始位置向东的公里数。

当且仅当你可以在所有给定的行程中接送所有乘客时，返回 true，否则请返回 false。

暴力思路

使用暴力的模拟思路，大概可以写成这样：

class Solution {
    public boolean carPooling(int[][] trips, int capacity) {
        int[] nums = new int[1001]; // 题目数据范围较小，直接开一个数组
        int mx_stop = -1;

        for (int[] trip: trips) {
            int people = trip[0], s = trip[1], e = trip[2];
            mx_stop = Math.max(mx_stop, e);
            for (int i = s; i < e; i++) {
                nums[i] += people;
            }
        }

        for (int i = 0; i < mx_stop; i++) {
            if (nums[i] > capacity) return false;
        }
        return true;
    }
}

但是这样的时间复杂度是 $O(nm)$ ，其中 $n$ 是 trips 的长度， $m$ 是 trips 中的最大值，显然是不够优秀的。

差分数组

引入差分数组后，针对每一个 trip，我们只需要对 nums[s] 和 nums[e] 进行操作即可，这样就将 $O(m)$ 的操作降低到了 $O(1)$ 。

class Solution:
    def carPooling(self, trips: List[List[int]], capacity: int) -> bool:
        d = [0] * 1001
        for num, from_, to in trips:
            d[from_] += num
            d[to] -= num
        return all(s <= capacity for s in accumulate(d))

1109. 航班预订统计

这里有 $n$ 个航班，它们分别从 $1$ 到 $n$ 进行编号。

有一份航班预订表 bookings ，表中第 $i$ 条预订记录 $bookings[i] = [first_i, last_i, seats_i]$ 意味着在从 $first_i$ 到 $last_i$ （包含 $first_i$ 和 $last_i$ ）的每个航班上预订了 $seats_i$ 个座位。

请你返回一个长度为 $n$ 的数组 $answer$ ，里面的元素是每个航班预定的座位总数。

思路

同样利用差分数组，对于每一个 booking，我们只需要对 d[first] 和 d[last + 1] 进行操作即可，这样就将 $O(m)$ 的操作降低到了 $O(1)$ 。
这里需要注意，需要额外判断 last + 1 是否越界，如果越界，则不需要对 d[last + 1] 进行操作。

class Solution:
    def corpFlightBookings(self, bookings: List[List[int]], n: int) -> List[int]:
        d = [0] * (n + 1)   # 多开一个位置，因为 index 从 1 开始，空一个元素 d[0] 不用转换下标

        for f, l, s in bookings:
            d[f] += s
            if l != n:
                d[l + 1] -= s
        
        return list(accumulate(d))[1:]

或使用一个额外的位置记录 d[n]，这样就不需要判断 last + 1 是否越界了。

class Solution {
    public int[] corpFlightBookings(int[][] bookings, int n) {
        int[] d = new int[n + 2];   // 多开两个位置，一个用于从 1 开始，一个用于记录 d[n]
        for (int[] booking: bookings) {
            int s = booking[0], e = booking[1], num = booking[2];
            d[s] += num;
            d[e + 1] -= num;
        }
        for (int i = 1; i <= n; i++) {
            d[i] = d[i - 1] + d[i];
        }
        return Arrays.copyOfRange(d, 1, n + 1);
    }
}

2381. 字母移位 II

给你一个小写英文字母组成的字符串 s 和一个二维整数数组 shifts ，其中 $shifts[i] = [start_i, end_i, direction_i]$ 。对于每个 i ，将 s 中从下标 $start_i$ 到下标 $end_i$ （两者都包含）所有字符都进行移位运算，如果 directioni = 1 将字符向后移位，如果 directioni = 0 将字符向前移位。

将一个字符向后移位的意思是将这个字符用字母表中下一个字母替换（字母表视为环绕的，所以 'z' 变成 'a'）。类似的，将一个字符向前移位的意思是将这个字符用字母表中前一个字母替换（字母表是环绕的，所以 'a' 变成 'z' ）。

请你返回对 s 进行所有移位操作以后得到的最终字符串。

思路

c2i = {c: i for i, c in enumerate(ascii_lowercase)}

class Solution:
    def shiftingLetters(self, s: str, shifts: List[List[int]]) -> str:
        diff = [0] * (len(s) + 1)
        for start, end, dir in shifts:
            diff[start] += dir * 2 - 1
            diff[end + 1] -= dir * 2 - 1
        return ''.join(ascii_lowercase[(c2i[c] + shift) % 26] for c, shift in zip(s, accumulate(diff)))

2132. 用邮票贴满网格图

给你一个 m x n 的二进制矩阵 grid ，每个格子要么为 0 （空）要么为 1 （被占据）。

给你邮票的尺寸为 $stampHeight \times stampWidth$ 。我们想将邮票贴进二进制矩阵中，且满足以下限制和要求：

覆盖所有空格子。不覆盖任何被占据的格子。我们可以放入任意数目的邮票。邮票可以相互有重叠部分。邮票不允许旋转。邮票必须完全在矩阵内。如果在满足上述要求的前提下，可以放入邮票，请返回 true ，否则返回 false 。

思路

这个题非常有意思，用到了二维前缀和和二维差分数组。
先来简单理解一下二维差分数组：

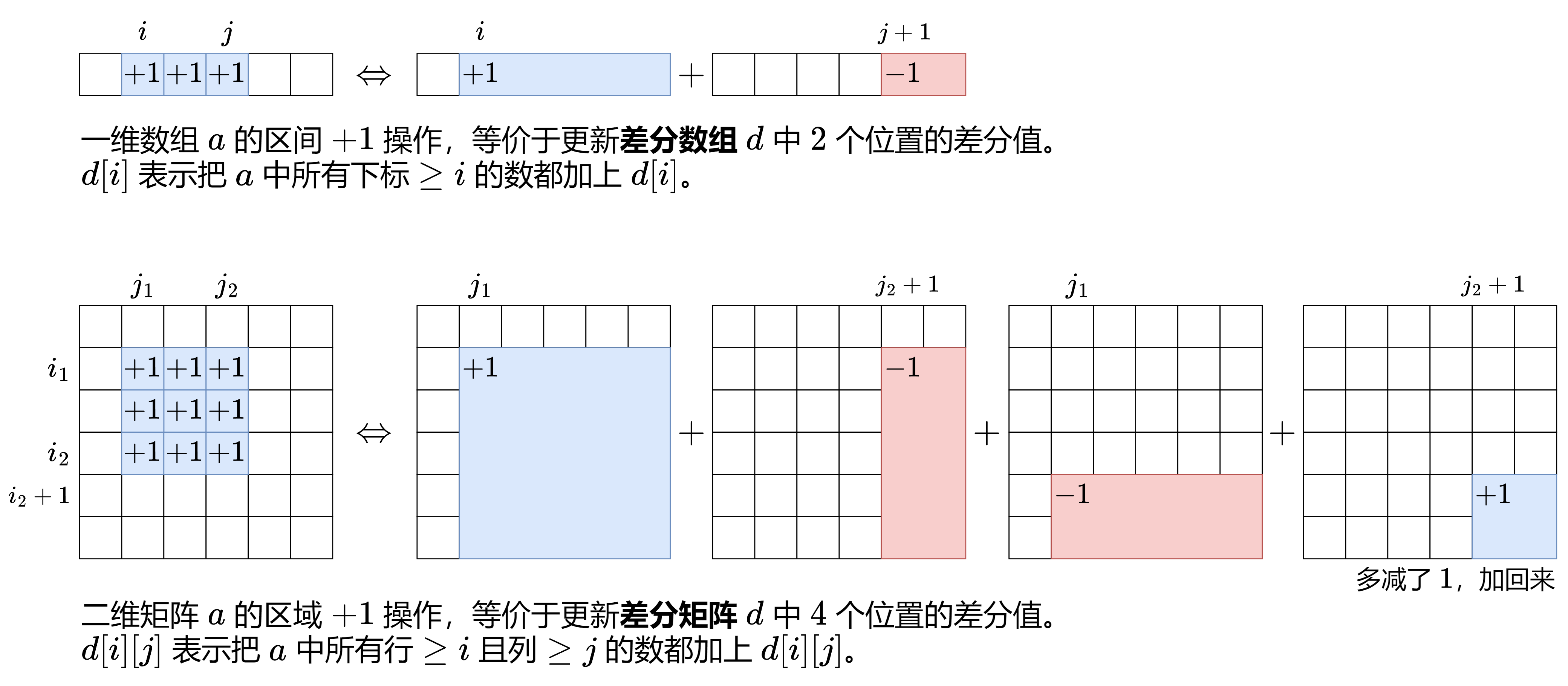
二维差分数组的作用是，对于一个子矩阵，我们可以通过对矩阵的四个角进行操作，来对子矩阵内的所有元素进行操作，将 $O(nm)$ 的操作降低到 $O(1)$ 。

这个题目中，可以发现每个格子都处在连续的 $stampHeight \times stampWidth$ 的子矩阵内，是整个网格都可以被覆盖的充要条件。有了这个发现，我们只需要判断是否每个格子都处在连续的 $stampHeight \times stampWidth$ 的子矩阵内即可。

首先我们为了在 $O(1)$ 的时间内判断一个格子是否处在连续的 $stampHeight \times stampWidth$ 的子矩阵内，需要使用二维前缀和。（使用二维前缀和快速寻找可贴位置）
我们使用一个二维差分数组，在 $O(1)$ 的时间内对每个可以放置邮票的格子记录其被覆盖的次数。（使用二维差分数组快速维护被覆盖的次数）
最后，我们遍历每个格子，判断其是否被覆盖，如果没有被覆盖，则返回 false。这一步可以在二维差分数组上原地进行，不需要额外的空间。

class Solution:
    def possibleToStamp(self, grid: List[List[int]], stampHeight: int, stampWidth: int) -> bool:
        m, n = len(grid), len(grid[0])

        # 1. 计算 grid 的二维前缀和
        # 前缀和需要在最开始多加一行一列，不需要特判开头元素
        s = [[0] * (n + 1) for _ in range(m + 1)]
        for i, row in enumerate(grid):
            for j, v in enumerate(row):
                s[i + 1][j + 1] = s[i + 1][j] + s[i][j + 1] - s[i][j] + v

        # 2. 计算二维差分
        # 为方便第 3 步的计算，在 d 数组的最上面和最左边各加了一行（列），所以下标要 +1
        # 差分数组需要在最后多一个元素，不需要特判结尾元素
        d = [[0] * (n + 2) for _ in range(m + 2)]
        for i2 in range(stampHeight, m + 1):
            for j2 in range(stampWidth, n + 1):
                i1 = i2 - stampHeight + 1
                j1 = j2 - stampWidth + 1
                if s[i2][j2] - s[i2][j1 - 1] - s[i1 - 1][j2] + s[i1 - 1][j1 - 1] == 0:
                    d[i1][j1] += 1
                    d[i1][j2 + 1] -= 1
                    d[i2 + 1][j1] -= 1
                    d[i2 + 1][j2 + 1] += 1

        # 3. 还原二维差分矩阵对应的计数矩阵（原地计算）
        for i, row in enumerate(grid):
            for j, v in enumerate(row):
                d[i + 1][j + 1] += d[i + 1][j] + d[i][j + 1] - d[i][j]
                if v == 0 and d[i + 1][j + 1] == 0:
                    return False
        return True

参考

灵茶山爱抚：【图解】从一维差分到二维差分（Python/Java/C++/Go/JS/Rust）