符号执行技术在如今软件测试领域受到了越来越多的关注，现在已经在测试和查找各种软件中的错误方面证明是有效的，这些软件低至低级网络和操作系统代码，高至高级应用程序代码。很幸运在与老师的接触中，了解到了符号执行领域相关的知识，这篇文章记录在阅读了相关领域的文章后的一些学习笔记。
在阅读了帝国理工大学的 Cristian Cadar 的 《Symbolic execution forsoftware testing: three decades later》[1] 后，我对符号执行有了基本的认识，下面简述一下我的理解。

什么是符号执行

符号执行是一种软件测试技术，从名字出发，大概意思是指利用符号而不是具体数值作为输入，进行代码的执行。
符号执行相关思想在上世纪八十年代就被提出，而在近代，随着约束可解性的进展，符号执行也得以蓬勃发展。其最核心的思想是利用符号值（symbolic values）代替具体的输入，从而将变量的值用基于符号的符号表达式（symbolic expressoins）来表达，最后得到的输出也是一个关于符号的函数。

能干什么

作为一种软件测试技术，符号执行的关键目的是在给定的时间内探索（并检测）尽可能多的不同程序路径。

手动规范测试要求输入值是一笔很大的开销，且不能保证在测试期间观察到所有可能的行为。
为了改进观察到的行为范围（或测试覆盖范围），我们引入了各项技术，其中之一是随机生成潜在的测试数据，这种方法有着很明显的缺点：

• 一是很产生很多结果相同的冗余用例
• 二是想要尝试出会导致bug的输入用例的可能性非常小

而另一种提出的方法就是我们要说的符号执行。如上文所说，在符号执行中，我们使用符号变量代替输入值来执行程序。程序中的每个条件表达式都表示一个确定执行路径的约束。其目标是为输入生成具体的值，从而导向不同的路径。选择路径的策略对分析的质量有很大的影响，经典的方法是使用通过回溯对路径的深度优先探索。

而且符号执行具有能够生成高覆盖率测试用例和发现复杂应用中深层错误的特性，从生成测试用例和寻找程序缺陷两方面出发，符号执行的优势在于：

• 生成高覆盖率的测试用例
• 提供触发bug的具体输入

与其他程序分析技术相比，符号执行不限于查找缓冲区溢出等宽泛的错误，而是可以推理更高级的程序属性，如复杂的程序断言。

传统符号分析

在接触传统的符号分析之前，我们需要先明确几个概念。

执行路径

当我们在代码的执行过程中遇到程序分支时，我们将选择的布尔值连接，得到的就是我们走到当前路径点的执行路径，也就是说，执行路径就是一个由布尔值构成的序列，第i个值代表第i次分支的条件语句值。

执行树

执行路径通过树来表示。

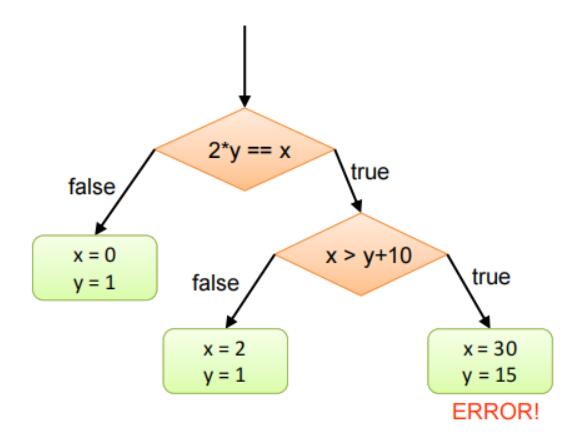
这里注意图中绿色方块中代表的就是对应路径下的一个case。
而我们在符号分析的过程中的目标，就是希望通过 constraint solver 得到的具体值，关于这些会在下文继续说明。

有了以上概念的补充，接下来我们可以进入传统的符号执行技术的具体定义。

组成

传统的符号执行主要包括两部分内容：

1. 一个符号状态 $\sigma$ ：就是一个映射（函数），初始为空，存放对应变量在当前执行路径下的表达式（如 {z→2y, z→y}）
2. 路径约束PC（path constraint）：针对对应执行路径下的路径限制，即需要满足的无量词一阶公式，初始为真。

这里需要解释一下所谓无量词一阶公式（quantifier-free first-order formula）
根据维基百科，First-order logic—also known as predicate logic ，这里的first-order指的是一阶逻辑，也就是谓词逻辑，与零阶逻辑（命题逻辑）区别
在离散数学的知识中，我们知道谓词逻辑中有存在量词（existential quantifier）和全称量词（universal quantifier），这里的无量词，也就是在约束PC中不能包括量词
综合上面的定义，无量词一阶公式，就是将命题用逻辑连接词析取、合取、非连接即可（不包括量词）。

我们在程序执行时，PC 和 $\sigma$ 随着程序的执行而更新，在一条路径的尽头，用constraint solver来解出一个约束对应的具体值，即可作为当前路径的输入。constraint solver 作为另一个研究领域，这里不再详细讨论。

在路径中，每遇到一个条件判断（if），第一条路径为真，PC更新为 PC ∧（命题为真条件），第二条为假，新增一个符号执行，加入 σ 并以 PC ∧（命题为假条件） 作为新的PC，这一步就是约束收集。直到路径出口或是遇到错误就可以利用 constraint solver 解出具体的值。

基本实现

关于基本实现的内容，我们可以在2010年卡耐基梅隆大学的一篇论文 All You Ever Wanted to Know about Dynamic Taint Analysis and Forward Symbolic Execution (but Might Have Been Afraid to Ask)[2] 中得到大概的认识，文中首先给出了一个简单语言 SIMPIL 的语法定义和操作语义。

上面三张图片定义的简单语言可以帮助我们更好地理解符号执行的具体方法，注意语法从下往上阅读。
要实现符号执行，我们只需要新加入一个上下文变量 $\Pi$，记载当前路径下的约束；

同时执行语义加以简单变动，更新变量 $\Pi$。

文中通过这样的语言定义针对具体的例子给出了如何创造一个简单的符号执行引擎，并提出了遇到的问题和一些简单的解决方案，这里不再展开，感兴趣的读者可以自行阅读。

另外，在具体的实现中还要注意在路径中遇到循环或是递归导致执行路径无限长的情况，需要加入限制，我们一般用超时、路径数量、循环迭代次数或探索的深度等指标加以限制，将无穷限制改为多个重复命题合取。
例：$N_i>0$为判断条件，当前的PC即可写为

限制

在传统的符号执行中，所有输入都用符号代替，可能遇到的最大的限制就是约束不可求解的问题，这里举两个情况：

1. 所执行的过程不可见（e.g.系统函数或闭源函数）；
2. 所执行的过程不能被constraint solver计算，可以假设不能进行非线性的运算。

以上两种情况，PC都不能被解出具体的数值，也就不能产生输出，为了解决这种问题，我们引出了现代的符号分析技术，以及其为了缓解不可解问题做出的取舍。　　

---

现代符号分析技术

现代符号分析技术的重要特性就是具体值和符号执行的混合，也称动态符号分析技术。

Concolic测试：导向性随机测试（DART）

以Concolic测试为例，在执行向下探索时，除了传统的符号状态 $\sigma$，还会保存一个具体值的映射，映射的具体值也会在路径更新时通过 constraint solver 更新。
需要注意的是由于Concolic测试需要维护具体值，需要初始具体的值（指定或随机）。

执行生成测试（EGT）

EGT的本质还是具体值和符号执行的混合，他的具体操作方式是区分程序的具体状态和符号状态来工作：在每次执行前，检查值是否为具体的，如果是具体值，直接运算，否则，如果至少有一个值是符号值，就通过符号执行。
因此，在需要具体值时，EGT可以随时通过约束计算出一个具体值代入，这一点与Concolic测试一直维护一个具体值的映射做区别。

---

综上，在现代符号执行技术中，由于采用了混合具体状态和符号状态，需要着重注意的一点就是如何做出权衡：
在与外界函数或者约束不可解的问题打交道时，动态符号执行采取的策略是利用具体值代替符号值，这样的问题就是可能会导致路径的丢失、完整性下降，所以必须要做出相应的权衡。

挑战和一些解决方法

在代码执行技术领域，目前遇到的主要挑战可分为以下三个：

路径爆炸

这主要是指由于动态符号执行的过滤能力不足，程序中路径的指数型增长爆炸问题，当前比较流行的解决方案有：

• 启发式技术对路径划定优先级
  主要利用随机探索或其他手段优先选择一些路径
• 程序分析技术（减少程序复杂性）
  1. 静态合并一些路径，由于时间限制，具体采取的技术暂且不谈
  2. 缓存和重用后续计算中的低级函数分析来改进符号执行，大概思想是重用类似属性的简单函数结果到复杂函数中（存疑）
  3. 在路径探索过程中剪枝，删去冗余路径（如同一个程序点下约束相同的输入）

约束求解

上面说符号执行是在约束求解领域取得快速进展后快速发展，而实际上约束求解问题仍是现在符号执行领域最主要的瓶颈之一。
下面介绍两种具有代表性的优化：

1. 不相关约束消除：
   对于当前分支约束求传递闭包，与当前分支无关的变量可忽视。
2. 增量求解：
   缓存之前的限制和求解具体值，子集直接使用，超集判断是否可用（通常可用）。

内存建模

将程序语句转换为符号约束的精度会对符号执行实现的覆盖范围以及约束求解的可伸缩性产生显著影响。例如，使用实际整数代替内存中的定长证书数学模型可能有效，但可能会导致例如溢出等的边界用例的不精确问题。

还有对于指针问题的约束求解，一类代表是像DART这样的系统，它只解决具体指针的问题，或者像CUTE和CREST这样只支持指针的相等和不等的约束的系统，这类系统难题已被很好解决。另一类是EXE等使用数组理论来建模指针的基于STP或Z3这样的求解器实现的系统。

同时应该非常注重在精度和约束求解的伸缩性之间的权衡，这种权衡常常基于被分析的代码的规模以及其处于系统中的层次。

并发问题

由于并发程序不确定性的内在属性，对并发程序的测试往往非常困难。尽管存在这些挑战，但动态符号执行已被有效地用于测试并发程序，包括具有复杂数据输入的系统、分布式系统和GPGPU应用程序。

---

以上就是代码执行技术领域，目前遇到的主要挑战。

参考文献：

[1]Cadar C, Sen K. Symbolic execution for software testing: three decades later[J]. Communications of the ACM, 2013, 56(2): 82-90.

[2] Schwartz E J , Avgerinos T , Brumley D . All You Ever Wanted to Know about Dynamic Taint Analysis and Forward Symbolic Execution (but Might Have Been Afraid to Ask)[C]// 31st IEEE Symposium on Security and Privacy, S&P 2010, 16-19 May 2010, Berleley/Oakland, California, USA. IEEE, 2010.