avatar

🧊foril

giteegiteegiteegitee
avatar

🧊foril

红黑树

2024-03-14 -

红黑树其实就是一种 独立的自平衡二叉搜索树，通过一些规则来维护树的平衡，从而保证在最坏情况下依旧能够提供近似于对数时间的增删查操作性能。

作为一颗搜索树，他的作用当然是提供快速的查找操作。
在 Java8 以前，Java 中 HashMap 的底层实现是数组+链表，当哈希冲突时，会将冲突的元素放到链表中，但当哈希表变得非常不平衡时，特别是当很多键都映射到同一个哈希时，链表的效率会降低到线性时间，这意味着操作的时间复杂度会退化到 O(n)O(n)。为了优化这种极端情况的性能，Java8 引入了红黑树来优化长链表的情况。当链表的长度超过某个阈值（默认是 TREEIFY_THRESHOLD，值为 8）时，链表会被转换成红黑树，这样即使在最坏的情况下，操作的时间复杂度也可以保持在 O(log⁡n)O(\log n)。这种优化显著提高了 HashMap 在不平衡数据分布情况下的性能。

红黑树为什么这么设计？

刚才说到红黑树被设计为一种 独立的自平衡二叉搜索树，那他自然需要采用一些规则来维护树的平衡，而这些规则的灵感就是来自于 2-3-4 树。

因此可以说 2-3-4 树是红黑树的概念模型，红黑树可以被视为 2-3-4 树的一种二叉树实现，其设计原则和操作反映了 2-3-4 树的性质和平衡机制。
这种关系不仅可以帮助我们理解红黑树的工作原理，而且也说明了红黑树是如何通过二叉树结构来模拟 2-3-4 树的行为的。

理解红黑树

这里贴上红黑树的发明人 Sedgewick 的讲解视频，这个视频以 2-3 树为例（其实就是简化讲解了红黑树的概念），讲解了红黑树的设计原则和操作，非常值得一看。接下来我会加入一些我的个人理解，总结一下红黑树是怎么通过二叉树来实现 2-3 树的。

2-3 树的表示

首先，我们需要定义一个二叉树如何表示一个 2-3 树。这里我们引入了红连接的概念：一个红连接只能作为父节点的左子树出现（left-leaning links），在红黑树中，代表的就是与其父节点在 2-3 树中是同一个 3 节点内的数字：

红连接

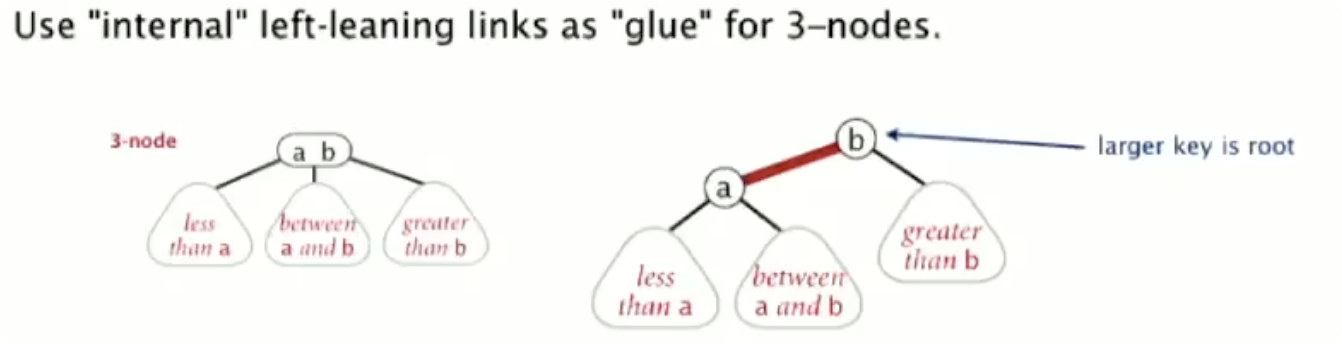
所以如果我们将所有的红连接顺时针旋转至水平，那么我们就可以得到一个叶节点都在同一层的 2-3 树。

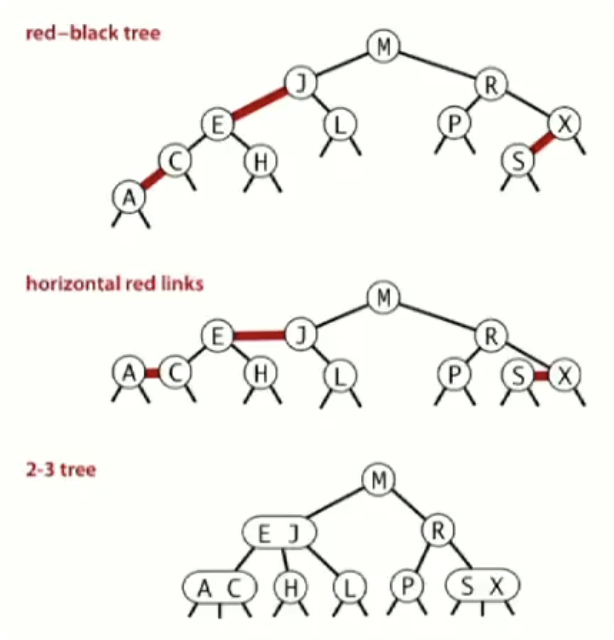
红黑树旋转

在这个得到的红黑树中，对于一个关键字的查找与在一个平衡搜索数中的操作是一模一样的。

public Value get(Key key) {
    Node x = root;
    while (x != null) {
        int cmp = key.compareTo(x.key);
        if (cmp < 0) x = x.left;
        else if (cmp > 0) x = x.right;
        else return x.val;
    }
    return null;
}

由于每个连接只和一个节点相关联，所以我们可以 将连接的颜色放进节点中，只需要在节点中增加一个布尔值来表示连接的颜色即可。

private static final boolean RED = true;
private static final boolean BLACK = false;

private class Node {
    Key key;
    Value val;
    Node left, right;
    boolean color;
}

private boolean isRed(Node x) {
    if (x == null) return false;
    return x.color == RED;
}

红黑树的基本操作

接下来我们需要介绍三个红黑树的基本操作：左旋、右旋和颜色翻转。通过这三个操作，我们可以在红黑树中实现 2-3 树的插入并保持树的平衡。

左旋

左旋是指将一个红色右连接（right-leaning links）变为左连接。这个操作的目的是为了将红色右链接变为左链接，从而符合我们对于红黑树模拟 2-3 树的定义。

private Node rotateLeft(Node h) {
    Node x = h.right;
    h.right = x.left;
    x.left = h;
    x.color = h.color;
    h.color = RED;
    return x;
}
左旋

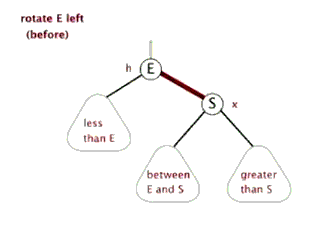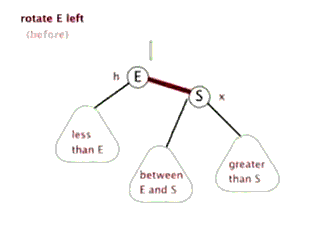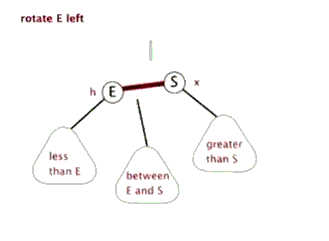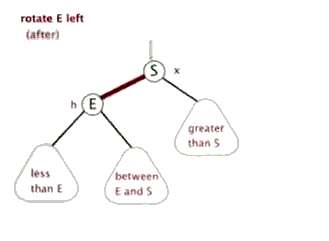
同理，在一些连续两个红连接的情况下，我们可以通过右旋来将红连接变为左连接。

private Node rotateRight(Node h) {
    Node x = h.left;
    h.left = x.right;
    x.right = h;
    x.color = h.color;
    h.color = RED;
    return x;
}
右旋

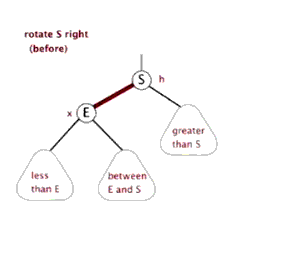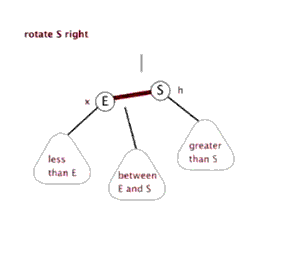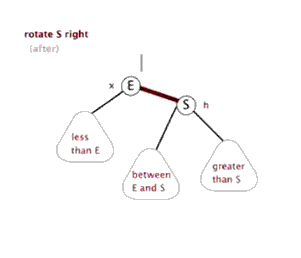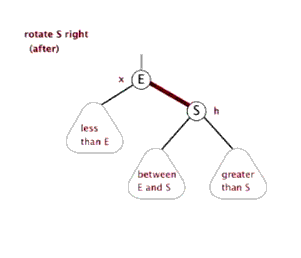
颜色翻转

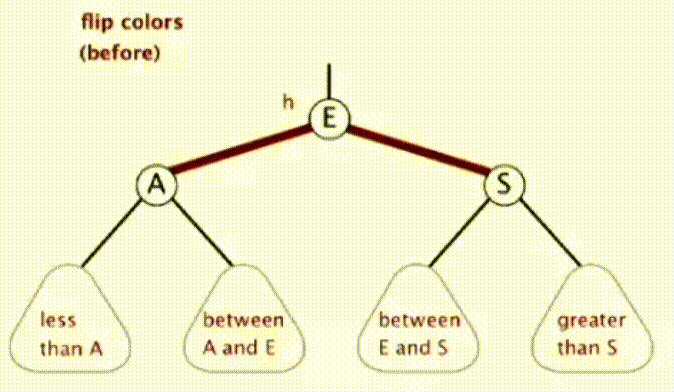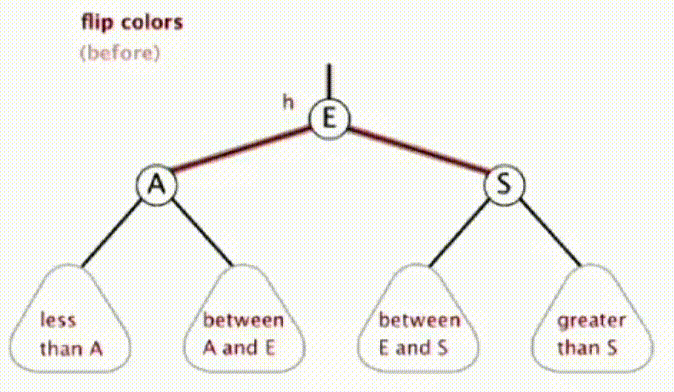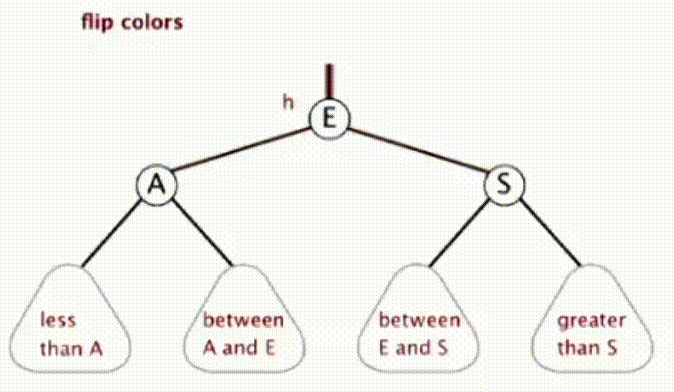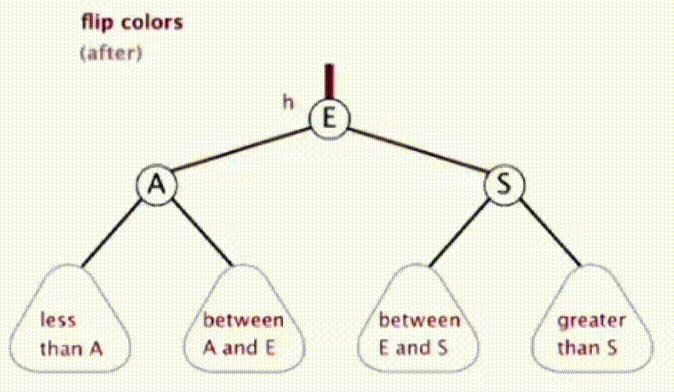
当一个 2 节点左右儿子都是红连接时，其实对应在 2-3 树中就是一个临时 4 节点，我们需要将这个 3 个数字的中间提到上一层，其实就是将这个 4 节点的中间数字变为红色，两边的数字变为黑色。这就需要颜色翻转操作

private void flipColors(Node h) {
    h.color = RED;
    h.left.color = BLACK;
    h.right.color = BLACK;
}·
颜色翻转

红黑树的插入操作

有了上面三个基本操作，我们的目标就是通过这些操作，时刻维护插入或删除节点时我们的 红黑树和相应操作后得到的 2-3 树有一一对应的关系。

接下来分情况讨论红黑树会遇到的插入情况。

  1. 插入一个 3 节点的左边：右旋
  2. 插入一个 3 节点的中间：左旋 + 右旋
  3. 插入一个 3 节点的右边：颜色翻转
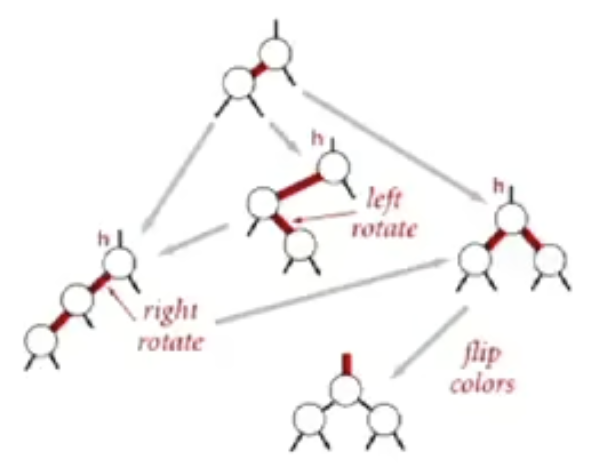
红黑树插入

于是我们在整个红黑树的插入操作可以总结为：

  1. 正常的二叉树插入操作，新节点总是红色
  2. 插入后右子节点是红色，左子节点是黑色，进行左旋
  3. 左孩子和左孩子的左孩子都是红色，进行右旋
  4. 两个孩子都是红色，进行颜色翻转
private Node put(Node h, Key key, Value val) {
    if (h == null) return new Node(key, val, RED);
    int cmp = key.compareTo(h.key);
    if (cmp < 0) h.left = put(h.left, key, val);
    else if (cmp > 0) h.right = put(h.right, key, val);
    else h.val = val;

    if (isRed(h.right) && !isRed(h.left)) h = rotateLeft(h);
    if (isRed(h.left) && isRed(h.left.left)) h = rotateRight(h);
    if (isRed(h.left) && isRed(h.right)) flipColors(h);

    return h;
}

特征

了解了以上内容，我们就可以更好地理解红黑树的特征了。

  1. 节点颜色有红色和黑色
  2. 根节点必为黑色
  3. 任意节点到叶子节点经过的黑色节点数目相同

    只有黑色节点才会在 2-3 树中真正贡献高度，2-3 树中所有叶子节点都在同一层。

  4. 不会有连续的红色节点

总结

红黑树是一种非常优秀的数据结构，通过左旋、右旋和颜色翻转来维护平衡搜索树的平衡，这些操作可以保证红黑树的高度始终保持在 O(log⁡n)O(\log n)，从而保证了红黑树在最坏情况下依旧能够提供近似于对数时间的增删查操作性能。